Criterios de congruencia de Triángulos
Son postulados que permiten establecer si dos triángulos son congruentes a partir de algunas de las medidas de sus lados o sus ángulos.
1. Criterio: Lado - Lado - Lado (LLL)
Dos triángulos son congruentes si tienen sus tres lados congruentes.
2. Criterio: Lado - Ángulo - Lado (LAL)
Dos triángulos son congruentes si sus dos lados y el ángulo comprendido entre ellos son congruentes.
3. Criterio: Ángulo - Lado - Ángulo (ALA)
Dos triángulos son congruentes si sus dos ángulos y el lado común son congruentes.
Ejemplo 1
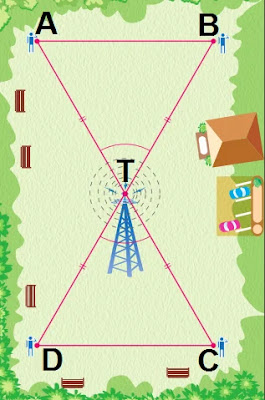
En la Figura 1 se
observa la ubicación de una antena.
Figura 1
En los puntos A, B, C y D
Los triángulos ∆ABT y ∆DCT determinados en la Figura 1 son congruentes por el criterio LAL. Observa la Figura 2.
Ejemplo 2
Observa la Figura 3 y
comprueba que el triángulo ABC es
congruente con el triángulo DEF
Figura 3






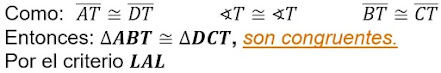




No hay comentarios:
Publicar un comentario